Általános párhuzamos program
A Programozás elméletben adatközpontú megközelítést alkalmazunk. Ezzel a megközelítéssel mind a feladat, mind a program, stb. definícióját adatok halmazán, állapottér meghatározásával írjuk le.
Egy adat típus-értékhalmaza az adat lehetséges értékeiből áll. Állapotnak hívjuk azt az érték-együttest, amikor egy feladat vagy egy program minden adata felvesz a saját típus-értékhalmazából egy-egy értéket.
Formálisan:
Legyenek \(A_1, ... , A_n (n\in\mathbb{N}^+)\) típusérték-halmazok, és a halmazokat azonosító (egyedi, páronként különböző) \(v_1, ... , v_n\) címkék (változók)
Minden cimke egy adatot (változó) jelöl. Egy állapot \(\{v_1:a_1, ... , v_n:a_n\}\) (cimkézett értékek halmaza), ahol minden változó felvesz egy értéket a hozzátartozó típus-értékhalmazból. (\(a_i\in A_i\))
Az összes így képzett állapot halmazát állapottérnek nevezzük:
\[A := \{ \ \{v_1:a_1, ... ,v_n:a_n\} \ | \ a_i\in A_i \ (i=1,...,n) \ \}\]
A feladat egy kapcsolat (leképezés) a bemenet és az eredmény között: \(F \subseteq A \times A\)
Figyeljük meg, hogy az \(F\) reláció csak része az \(A\times A\) descartes-szorzatnak. Mivel azonban a kiinduló állapotok csak az állapottér egy részhalmazát képzik, illetve az ezekhez rendelt állapotok ugyancsak az állapottérnek egy részhalmazát képzik, így érthető, hogy a feladat nem feltétlenül érvényes a teljes állapottéren.
Példa:
Osztója reláció
Kérdés: \(d\) osztója-e \(n\)-nek, melyet az \(l\) logikai változó jelöl.
\[\begin{align} A & = ( n:\mathbb{Z}, d:\mathbb{Z}, l:\mathbb{L} ) \\ F & \subseteq A \times A \\ & \text{ahol} \\ D_f & = \{\{n,d,l\} \in A \ | \ d \neq 0 \} \\ \forall a & \in D_F : F(a) = \{ \{n, d, l\} \in A \ | \ l = d|n \} \end{align}\]Tehát láthatjuk, hogy az \(F\) értelmezési tartományába csak azok az állapotok tartoznak bele, ahol az osztó nemnulla. Az \(l\) változó értéke \(F(a)\)-ban pedig aszerint alakul, hogy az \(d\) osztja-e \(n\)-et.
Válasszunk egy \(P\) paraméterhalmazt, mellyel az \(F\) feladat felbontható két reláció kompozíciójára: \[F = F_1 \circ F_2\] ahol \(F_1 \subseteq A \times P\) és \(F_2 \subseteq P \times A\), úgy hogy: \(\forall a \in D_F: F(a) = F_2(F_1(a))\)
Ekkor definiálni tudjuk a feladat elő- és utófeltételét:
\(\forall p \in P:\)
Jelölés magyarázat:
Ha adott egy \(Q : A \rightarrow \mathbb{L}\) állítás, annak az igazsághalmaza: \([Q] := \{q \in Q \ | \ Q(a) \ igaz \}\). Tehát \(Ef\) olyan állítás, mely a feladat minden kezdőállapotára igazat ad, illetve az \(Uf\) olyan állítás, mely az \(F(a)\) állaptokra ad igaz értéket.
Egy programot sokféleképpen lehet megadni. (program-gráf, strukogram, automaták, utasítások, pszeudo- vagy programnyelv).
A program alaptermészete az, hogy különböző végrehajtásokat okoz. Tehát egy program a lehetséges végrehajtásainak összessége. Egy ilyen végrehajtás sorozatos állapot-változásokat idéz elő, ennél fogva leírható egy állapotsorozattal.
Példa:
\(A = (n : [-5, ..., \infty ) )\)
while n != 10:
n = n + sgn(n)Ennek a lehetséges végrehajtásai a következők:
0: <0,0,0,0,0, ... > nem terminál (divergál)
4: <4,5,6,7,8,9,10> terminál
10: <10> terminál
13: <13,14,15,16, ... > nem terminál (divergál)
-2: <-2,-3,-4,-5, fail > abortálA program lehet nem-determinisztikus (nem mindig ugyanazt az állaposorozatot adja a kezdőállapból indítva), lehetnek segédváltozói, lehet véges vagy végtelen hosszú, illetve leállhat hibás állapotban vagy speciálisan holtpontban.
A program alap-állapottere a program interfésze, mellyel a program a környezetével kommunikál (kezdőállapotát a környezet adja, végállapotát a környezet kapja). Illetve ez írja le a program alap-változóit, melyek a program működése során végig léteznek.
\[ \overline{A} := \bigcup_{A \leq B} B \]
Ezek alapján a \(A\) feletti programnak hívjuk azt az \[ S\subseteq A \times (\overline{A} \cup \text{fail} )^{**} \]
relációt, melyre fennállnak a következők:
\(D_S = A\)
a program értelmezési tartománya az alap-állapottér.\(\forall a \in A : \forall \alpha \in S(a): \ |\alpha| \geq 1 \land \alpha_1 = a\)
az állapotsorozat legalább egy hosszú és a első állapota mindig az alap-állapottérből való.\(\forall \alpha \in R_S : \forall i \ (1 \leq i < |\alpha| ) : \alpha_i \neq \text{fail}\)
csak az utolsó elem lehetfail a végrehajtási állapotsorozatban\(\forall \alpha \in R_S : |\alpha| < \infty \longrightarrow \alpha_{|\alpha|} \in A \cup \{\text{fail} \}\)
a véges végrehajtások utolsó állapota vagy a fail vagy alap-állapottérbeli állapot.
Egy program akkor old meg egy feladatot (a program helyes a feladat szempontjából), ha végrehajtásai a feladat kezdőállapotaiból indulva a feladat megfelelő célállapotaiban állnak meg. Ekkor a feladat állapottere és a program alap-állapottere azonos kell legyen. Ilyenkor a program végrehajtásai között találjuk a feladat kezdőállapotából induló végrehajtásokat, amelyekről azt kell eldönteni, hogy terminálnak-e (hibátlan és véges hosszú) és végállapotuk a feladat által megkívánt valamelyik célállapot lesz-e.
Az üres program gyakorlatilag az identitásfüggvény. ( \(S := skip\) ) \[skip(\sigma) = <\sigma>\] (Azaz az üres program egyetlen állapota a kezdőállapot.)
A szekvenciával két program összefűzését érhetjük el.
Legyen \(S_1\) és \(S_2\) közös állapotterű (\(A\)) programok.
\[\begin{align} (S_1;S_2)(\sigma) & = \{ \alpha \ | \ \alpha \in S_1(\sigma)\cap \overline{A}^{\infty} \} \\ & \cup \{ \alpha \ | \ \alpha \in S_1(\sigma) \text{ és } |\alpha| < \infty \text{ és } \alpha_{|\alpha|} = \text{fail} \} \\ & \cup \{ \alpha \otimes \beta \ | \ \alpha \in S_1(\sigma) \cap \overline{A}^{\star} \text{ és } \beta \in S_2(\alpha_{|\alpha|}) \} \\ \end{align}\]Tehát:
Az elágazással feltételek alapján változtathatjuk a sorozatot.
Legyenek \(S_1 , ... , S_n\) programok és \(\pi_1 , ... , \pi_n\) feltételek, amelyeknek közös alap-állapottere az \(A\).
\[\begin{align} (\text{if } \pi_1 \rightarrow S_1 , ... , \pi_n \rightarrow S_n \text{ fi} )(\sigma) & = \\ \bigcup_{\substack{i=1 \\ \sigma \in D_{\pi_i} \land \pi_i(\sigma)}}^n S_i(\sigma) \ & \cup \ \begin{cases} <\sigma, \text{fail}> \quad \text{ha } & \exists i \in [1..n]: \sigma \notin D_{\pi_i} \ \lor\\ & \lor \ \forall i \in [1..n] : \sigma \in D_{\pi_i} \land \lnot\pi_i(\sigma) \\ \emptyset \text{ különben}\end{cases} \end{align}\]Tehát:
A ciklussal ismétlődő sorozatokat állíthatunk elő.
Legyen \(S_0\) program és \(\pi\) feltétel, amelyeknek közös alap-állapottere az \(A\).
\[\begin{align} (\text{while } \pi \text{ do } S_0 \text{ od})(\sigma) = \begin{cases} (S_0 ; \text{while } \pi \text{ do } S_0 \text{ od})(\sigma) \quad & \text{ha } \sigma \in D_\pi \land \pi(\sigma) \\ <\sigma> \quad & \text{ha } \sigma \in D_\pi \land \lnot\pi(\sigma) \\ <\sigma, \text{fail}> \quad & \text{ha } \sigma \notin D_\pi \end{cases} \end{align}\]Tehát:
skip-et hajtunk végreAtomi utasításnak párhuzamos/konkurens programok esetén tulajdonítunk fontos szerepet. Az atomi utasítás nem tartalmazhat sem ciklust, sem várakozó utasítást. Ekkor az utasítást egyszerre, megszakítás nélkül kell végrehajtani.
\[ [S](\sigma) = S(\sigma)\]
Elsőre furának tűnhet, de szemantikai értelemben valóban nincs különbség.
A várakozó utasítás párhuzamos/konkurens programok esetén szinkronizációra használható.
\[(\text{await }\beta\text{ then } S \text{ ta})(\sigma) = \begin{cases} <\sigma, \text{fail}> \quad & \text{ ha } \sigma \notin D_\beta \\ S(\sigma) \quad & \text{ ha } \sigma \in D_\beta \land \beta(\sigma)\\ (\text{await }\beta\text{ then } S \text{ ta})(\sigma) \quad & \text{ ha } \sigma \in D_\beta \land \lnot\beta(\sigma) \end{cases}\]
A harmadik esetben nem párhuzamos program esetén nincs, ami megváltoztassa a \(\sigma\) értékét, így ez holtpontot okozhat. A várakozó utasítás esetén a \(\beta\) kiétékelése és az \(S\) program atomi műveletként hajtódik végre. Az \(S\) nem tartalmaz sem ciklust, sem várakozó utasítást.
A párhuzamos blokkokkal leírhatjuk, hogy melyik programrészek futhatnak párhuzamosan.
Legyen \(S_1, ... , S_n\) a párhuzamosan végrehajtott program ún. programágai. Az ütemező ezek közül választhat egyet végrehajtásra.
Amennyiben az ütemező az \(i\)-edig ágnak adja a vezérlést:
\[\begin{align} (\text{parbegin } & S_1 \lVert ... \lVert S_i \lVert ... \lVert S_n \text{ parend})(\sigma) = \\ & \begin{cases} (\text{parbegin } S_1 \lVert ... \lVert S_{i-1} \lVert S_{i+1} \lVert ... \lVert S_n \text{ parend})(\sigma) & \quad \text{ha } S_i = \text{skip}\\ (u;\text{parbegin } S_1 \lVert ... \lVert S_{i-1} \lVert T_{i} \lVert S_{i+1} \lVert ... \lVert S_n \text{ parend})(\sigma) & \quad \text{ha } \text{skip} \neq S_i = u;T_i \\ \end{cases} \end{align}\]A strukturált programok helyesség bizonyításának lényege, hogy belássuk, a program megoldja az adott feladatot. Hoare egy olyan deduktív módszert javasolt, mely:
Jelöljük egy feladat specifikációját \((A, Q, R)\)-el, ahol \(A\) az alap-állapottér, \(Q\) az előfeltétel, és \(R\) az utófeltétel.
\[\{\{R\}\} \text{ skip } \{\{R\}\}\]
\[\frac{Q \Rightarrow R}{\{\{Q\}\} \text{ skip } \{\{R\}\}}\]
\[\{\{ v\in D_f \land \forall e \in f(v) : R^{v \leftarrow e} \}\} \ v:=f(v) \ \{\{R\}\}\]
Ez a következtetés talán némi magyarázatra szorul. A gondolat az egész mögött az, hogy végezzük el az utófeltételben a helyettesítést és az így kapott állítás lesz az előfeltétele az értékadásnak.
Nezzünk erre egy példát. Tegyük fel, hogy az értékadás: \(x:=5\), illetve az utófeltétel: \(R \ := \ 0<x<y\)
Ekkor \(R^{x\leftarrow 5} = 0<5<y = 5<y\) az előfeltétel, hiszen annak, hogy a program lefutása után \(0<x<y\) fennáljon egyedül az a feltétele, hogy \(5<y\), mivel az \(x\)-et a program meghatározza. A definíció ezt még megszorítja azzal, hogy:
\[ \frac{Q \Rightarrow v\in D_f \land \forall e \in f(v) : R^{v \leftarrow e}}{\{\{ Q \}\} \ v:=f(v) \ \{\{R\}\}} \]
Megjegyzés: speciális esetekben egyszerűsödhet az előfeltétel. Ha \(D_f = A\), akkor a \(v\in D_f\) feltétel elhagyható, ha pedig az értékadás determinisztikus, akkor a \(\forall e \in f(v):R^{v\leftarrow e}\) helyett elég \(R^{v\leftarrow f(v)}\)-t írni.
Legyen \(S_1\) és \(S_2\) programok szekvenciája az \(A\) alap-állapottéren az \((S_1;S_2)\).
Ha \(S_1\) az \((A, Q, Q')\) feladatot és \(S_2\) az \((A, Q', R)\) feladatot oldja meg, akkor a szekvencia megoldja az \((A, Q, R)\) feladatot.
\[\frac{ \{\{Q\}\} \ S_1 \ \{\{Q'\}\} \ \land \ \{\{Q'\}\} \ S_2 \ \{\{R\}\} }{ \{\{Q\}\} \ S_1;S_2 \ \{\{R\}\} }\]
Legyen az \(S_1 , ... , S_n\) programokból és a \(\pi_1 , … , \pi_n : A \rightarrow \mathbb{L}\) feltételekből álló elágazás az \(A\) alap-állapottéren az \(\text{if } \pi_1\rightarrow S_1 , ... , \pi_n \rightarrow S_n \text{ fi}\)
Ha minden \(Q\)-beli állapotra minden elágazás feltétel értelmes, és legalább az egyik teljesül is, továbbá minden \(S_i\) programág megoldja az \((A, Q\land\pi_i, R)\) feladatot, akkor az elágazás megoldja az \((A, Q, R)\) feladatot.
\[ \frac{ \substack{ Q\subseteq D_{\pi_1} \cap ... \cap D_{\pi_n} \\ Q \Rightarrow \pi_1 \lor ... \lor \pi_n \\ \forall i \in[1..n] : \ \{\{Q\land\pi_i\}\} \ S_i \ \{\{R\}\} } }{ \{\{ Q \}\} \ \text{if } \pi_1\rightarrow S_1 , ... , \pi_n \rightarrow S_n \text{ fi} \ \{\{R\}\} }\]
Tekintsük a \(\text{while } \pi \text{ do } S_0 \text{ od}\) ciklust az \(A\) alap-állapottéren, ahol \(S_0\) program a ciklusmag, a \(\pi: A \rightarrow \mathbb{L}\) a ciklusfeltétel. Továbbá legyen az ún. invariáns állítás egy \(I : A \rightarrow \mathbb{L}\) logikai függvény.
Ha:
Akkor a ciklus parciális értelemben megoldja az \((A,Q,R)\) feladatot.
\[\begin{align} & Q\Rightarrow I \\ & I \subseteq D_\pi \\ & I \land \lnot\pi \Rightarrow R \\ & \{I\land\pi\} \ S_0 \ \{I\} \\ \hline & \{Q\} \ \text{while } \pi \text{ do } S_0 \text{ od} \ \{R\} \end{align}\]A teljes helyességhez szükségünk van arra, hogy a ciklus leálljon. Ehhez be kell vezetnünk egy ún. variáns függvényt, vagy termináló függvényt: \(t : A \rightarrow W\), ahol \(W\)-n létezik egy \(< \ \subseteq W \times W\) rendezési reláció. Emellett \(W_< \subseteq W\) egy jólrendezett halmaz, azaz teljesen rendezett (bármely két elem összehasonlítható), és bármely (nemüres) részhalmazának van minimuma. A legtöbb esetben \(\mathbb{N} = W_< \subseteq W = \mathbb{Z}\) választással szoktunk éllni.
Megyjegyzés: a definíció bonyolultságát az indokolja, hogy a ciklus után a \(t\) értéke eggyel kisebb, mint a \(W_<\) minimuma, tehát a \(t\) értelmezési tartománya bővebb kell legyen, mint \(W_<\).
A parciális helyességen túl tehát azt kell még biztosítani, hogy \(S_0\) mellett a \(t\) szigorúan monoton csökkenő, azaz bármely \(a\in[I\land\pi]\) állapotból az \(S_0\) olyan \(b\in A\) állapotba jut, melyre \(t(b) < t(a)\). Amennyiben ez teljesül, akkor a ciklus megoldja az \((A, Q, R)\) feladatot.
\[\begin{align} & Q\Rightarrow I \\ & I \subseteq D_\pi \\ & I \land \lnot\pi \Rightarrow R \\ & I \land \pi \Rightarrow t \in W_< \\ & \forall c_0 \in W : \{\{ I\land\pi\land t = c_0 \}\} \ S_0 \ \{\{ I \land \ t<c_0 \}\} \\ \hline & \{\{Q\}\} \ \text{while } \pi \text{ do } S_0 \text{ od} \ \{\{ R \}\} \end{align}\]A párhuzamos programok helyesség-vizsgálatánál hasonlóan járunk el, mint nem párhuzamos estben. A gyengén teljes helyesség vizsgálatához ez elegendő is. A teljes helyességhez a holtpont-mentességet is vizsgálni kell majd.
Ahogy már korábban láttuk, az atomi utasítás szemantikája: \([S](\sigma) = S(\sigma)\).
Emiatt a szemantikából közvetlenül adódik a helyesség:
\[ \frac{ \{\{Q\}\} \ S \ \{\{R\}\} }{ \{\{Q\}\} \ [S] \ \{\{R\}\} } \]
Megjegyzés: A interferencia-mentesség és holtpont-mentesség jelen esetben biztosítva van, mivel az \(S\) atomi végrehajtású.
A várakozó utasítás (\(\text{await }\beta\text{ then } S \text{ ta}\)) szemantikájánál láttuk, hogy 3 eset lehetséges:
A helyesség kapcsán csak a harmadik pont érdekes, ami meg közvetlenül adódik.
\[ \frac{ \{\{Q \land \beta \}\} \ S \ \{\{ R \}\} }{ \{\{Q\}\} \ \text{await }\beta\text{ then } S \text{ ta} \ \{\{R\}\} }\]
Megjegyzés: A interferencia-mentesség és holtpont-mentesség jelen esetben biztosítva van, mivel \(\beta\) kiértékelése és \(S\) is atomi végrehajtású.
A párhuzamos blokk esetében azt tudjuk mondani, hogy ha \(S_1, ... , S_n\) interferencia-mentesek és a belőük képzett párhuzamos blokk holtpont-mentes, akkor:
\[\begin{align} & \{\{Q_1\}\} \ S_1 \{\{R_n\}\}, ... , \{\{Q_n\}\} \ S_n \{\{R_n\}\} \\ & Q \Rightarrow Q_1 \land ... \land Q_n \\ & R_1 \land ... \land R_n \Rightarrow R\\ \hline & \{\{Q\}\} \ \text{parbegin } S_1 \lVert ... \lVert S_n \text{ parend} \ \{\{R\}\} \end{align}\]Az \(S\) program segédállításokkal és \(S\) változóit nem értintő extra műveletekkel kiegészített változatát az \(S\) program annotációjának nevezzük és \(S^*\)-gal jelöljük. \[ \frac{ \{\{Q\}\} \ S^* \ \{\{R\}\} }{ \{\{Q\}\} \ S \ \{\{R\}\} } \]
kritikus utasítás: Értékadás, vagy értékadást is tartalmazó atomi művelet.
Egy \(u\) kritikus utasítás nem interferál a \(\{Q\} \ S^* \ \{R\}\) parciális helyességi tétellel, ha:
Ezek alapján a \(\{Q_k\} \ S_k^* \ \{R_k\} \ k\in [1..n]\) parciális helyességi tételek interferencia-mentesek, ha \(\forall i,j \in [1..n]: i\neq j\) folyamatpárra az \(S_i^*\)-nak egy kritikus utasítása sem interferál a \(\{Q_j\} \ S_j^* \ \{R_j\}\) parciális helyességi tétellel.
A parciális helyességi tételből kiindulva meg tudjuk határozni a gyengén teljes helyességi tételek interferencia-mentességét.
Tehát a fentiekhez hasonlóan, egy \(u\) kritikus utasítás nem interferál a \(\{\{Q\}\} \ S^* \ \{\{R\}\}\) gyengén teljes helyességi tétellel, ha:
Illetve hasonlóan a \(\{\{Q_k\}\} \ S_k^* \ \{\{R_k\}\} \ k\in [1..n]\) gyengén teljes helyességi tételek interferencia-mentesek, ha \(\forall i,j \in [1..n]: i\neq j\) folyamatpárra az \(S_i^*\)-nak egy kritikus utasítása sem interferál a \(\{\{Q_j\}\} \ S_j^* \ \{\{R_j\}\}\) gyengén teljes helyességi tétellel.
Blokkolt állapot: Egy párhuzamos program valamelyik folyamata blokkolt állapotba kerül, ha van benne egy várakozó utasítás, melynek előfeltétele \(Q\) és fennáll a \(Q \land \lnot \beta\).
Holtpont-állapot: Egy párhuzamos program holtpont állapotban van, ha legalább egy folyamata blokkolt, míg a többi vagy befejeződött, vagy azok is blokkoltak.
Holtpont-mentesség: Egy program egy állításra nézve holtpont-mentes, ha nincs olyan állapot, mely kielégíti az állítást viszont abból indítva a program holtpont-állapotba jut.
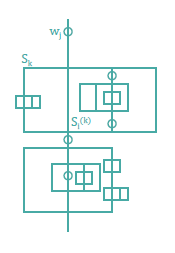
Az \(S\) párhuzamos program szerkezetének legfelső szintjén szekvenciálisan követik egymást (tetszőleges sorrendben) párhuzamos blokkok (\(S_k\)) és várakozó utasítások (\(w_j\)). Ezen felül a párhuzamos blokkok komponensei \(S_l^{(k)}\) is ugyanilyen szerkezetűek.

Általános párhuzamos program
Egy program akkor várakozik, ha:
\[D(S) = \Big( \bigvee_{j=1}^n (\text{pre}(w_j)\land\lnot\beta_j)\Big) \lor \Big(\bigvee_{k=1}^m D'(S_k)\Big) \]
Egy program a parbegin-parend blokkban akkor várakozik, vagy van legalább egy várakozó ága, miközben a többi végetért, vagy azok is várakoznak.
\[ D'(S_k) = \Big(\bigvee_{i=1}^l D(S_i^{(k)})\Big) \land \Big( \bigwedge_{i=1}^l (\text{post}(S_i^{(k)}) \lor D(S_i^{(k)}))\Big)\]
Ha \(D(S)\) hamis, akkor az \(S\) program holtpont-mentes.
Kritikus szakasz: Az interferencia vizsgálat szempontjából kritikusak egy folyamat azon utasításokból álló szakaszai (utasítás-szekvenciái) amelyek más párhuzamosan futó folyamatokkal közösen használnak egy erőforrást. Az ilyen kritikus szakaszoknak a működését az interferencia mentesség érdekében össze kell hangolni.
A kölcsönös kizárás egy adott erőforrás (erőforrás csoport) párhuzamos programbeli használatának egy lehetséges módja. Ennek során amíg egy folyamat egy adott közös erőforrás kritikus szakaszában van, addig a többi folyamat ugyanezen erőforrás kritikus szakaszában nem tartózkodhat: valami mást csinál vagy a kritikus szakaszba történő belépésre várakozik.
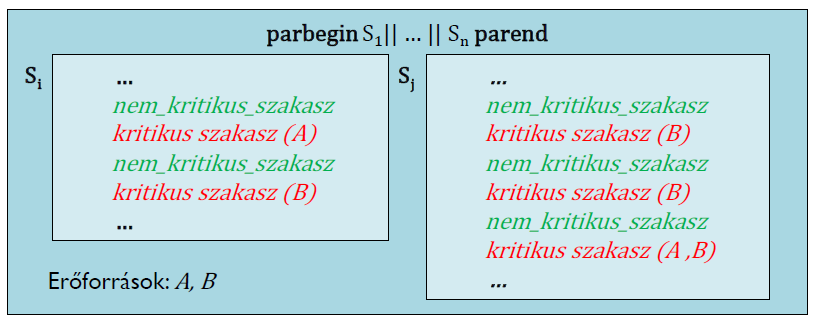
Kölcsönös kizárás
A kölcsönös kizárás megvalósításához a kritikus szakaszokat különleges belépő és kilépő szakaszokkal egészítjük ki, amelyek diszjunktak a folyamat többi részétől:
\[\big(\text{var}(\text{BK}_i) \cup \text{var}(\text{KK}_i) \big) \cap \big(\text{var}(\text{NK}_i) \cup \text{var}(\text{KS}_i) \big) = \emptyset\]
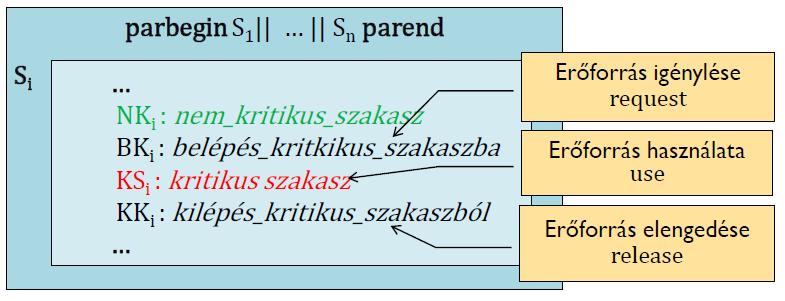
Kölcsönös kizárás megvalósítása
A kölcsönös kizárás akkor teljesül, ha: