S0-02 Típusmodellek (Programozás elmélet)

Tartalom

1. Absztrakt adattípus
2. Adattípus specifikációja
3. Adattípus osztály
4. Paraméterátadás
5. Reprezentációs függvény
6. Öröklődés és polimorfizmus
7. Liskov féle szubsztitúciós elv
8. További források

1. Absztrakt adattípus

Típus fogalma általában

Mi a típus? Biteken tárolt információk jelentése, illetve hogy hogyan kell értelmezni és módosítani őket

Típus fogalma formálisan

Egy

\[(A, F)\]

páros, ahol

• A: adattípust felépítő objektumok halmaza
• F: objektumokon értelmezett műveletek halmaza

Absztrakt adattípus (ADT)

• Szolgáltatásoknak egy halmaza, ahol a szolgáltatásokat egy megvalósító adattípus nyújtja

ADT specifikációja

• Szolgáltatások leírása, a specifikáció nem írja elő a megvalósítás módját

ADT megvalósítása

• ilyen szolgáltatásokat nyújtó adattípus

ADT korai és modernebb megközelítése

• Korai megközelítésben: azonos STRUKTÚRÁJÚ adatok (C struct-ok)
• Modern megközelítésben: azonos SZOLGÁLTATÁST nyújtó adatok (C++/Java/C# osztályok)

Szignatúra

• Programozási nyelvekben ez a deklarációnak felel meg
  • (Gondolj a függvény típusszignatúrájára Haskell-ben)
• \(\sum\) szignatúra egy \(\sum = (S, OP)\)
  • \(S = \{ S_0, S_1, ... , S_n \}\): szortok neveinek halmaza (fajták, alaptípusok)
  • \(OP = \{ f_0, f_1, ... , f_m \}\): művelet neveinek halmaza
• Az \(f_i\) művelet: egy \(f_i: s_{i_1} \times s_{i_2} \times \cdots s_{i_k} \rightarrow s_{i_0}\) parciális leképezés
  • (\(művelet: argumentum\ szortok \rightarrow target\ szortok\))
• Argumentum szortok (miből): \(s_{i_1} \times s_{i_2} \times \cdots s_{i_k}, \qquad k \geq 0\)
• Target szort (mibe): \(s_{i_0}\)

Lényeg: a műveletek szortokból szortokba képeznek le

Szignatúra algebra

• Ez az ami jelentést rendel a szignatúrához
• Programozási nyelvekben ez a definíciónak (implementációnak) felelne meg
• Az ADT lehetséges implementációját modellezi le
• \(\sum = (S, OP)\) szignatúrához tartozó algebra: \(\sum_A = (S_A, OP_A)\)
  • \(S_A = \{ A_{s_0}, A_{s_1}, \cdots A_{s_n} \}\): szortok, amikhez jelentések is tartoznak (hordozó halmaz)
  • \(OP_A = \{ f_0, f_1, ... , f_m \}\): műveletek, amikhez jelentések is tartoznak (függvények)
  • A \(f_i\) művelet: egy \(f_i: A_{s_{i_1}} \times A_{s_{i_2}} \times \cdots A_{s_{i_k}} \rightarrow A_{s_{i_0}}\) parciális leképezés
  • \(k = 0\) esetén \(f_i\) az \(A_{s_{i_0}}\) szort konstansa
• Szortok neveihez \(\leftarrow\) hordozó halmazt rendel
• Műveletek neveihez \(\leftarrow\) függvényeket rendel

2. Adattípus specifikácija

• Szignatúra és szignatúra algebra: lehet, hogy van két különböző módon viselkedő szignatúra algebra!
• Hogyan adjunk szemantikát ezekhez? Specifikációval.
• Specifikáció: szerződés a felhasználó és a megvalósító között
  • Legyen a lehető legáltalánosabb, hogy ne korlátozza a megvalósítást!

Absztrakt adattípus specifikációja

Specifikáció: \(SPEC = (\sum, E)\) (alternatív jelölés: \(SPEC = (S, OP, E)\))

• \(\sum\): szignatúra
• E: műveletek szemantikáját meghatározó specifikáció

Absztrakt adattípus specifikációk fajtái

1. Állapot elvű specifikáció (Hoare-féle módszer)

• Műveletek elő- és utófeltételeinek halmaza
• \(\{\varphi\} P \{\psi\}\)
  • \(\varphi\): előfeltétel
  • P: program
  • \(\psi\): utófeltétel

2. Procedurális specifikáció

• Műveletek kiszámítási szabályainak halmaza
• Függvény jelentésének, kiszámítási szabályának pszeudokód-szerű definiálása

3. Axiomatikus specifikáció (algebrai specifikáció)

• Eljárás jelentését meghatározó logikai állítások
• Függvények jelentését axiómákban írjuk le
• Axiomákat rendszerint predikátumokkal adjuk meg

Szignatúra algebrák közötti homomorfizmus

(morfizmus: leképezés)

• Alaphalmazok (S) és műveletek (OP)
• Legyen két szignatúra algebra:
  • \(\sum_A = (S_A, OP_A)\) és \(\sum_B = (S_B, OP_B)\)

\(h: A \rightarrow B\) egy függvénycsalád

1. Minden S-beli s szortra \(h_s: A_s \rightarrow B_s\)
   • azaz A szortját \(\rightarrow\) B megfelelő szortjára képezi le
2. \(\forall f_{A_i}\) és \(\forall (A_{s_{i_1}}, A_{s_{i_2}}, ..., A_{s_{i_k}})\) esetén: \(f_{B_i} megfelel f_{A_i}\)-nek
   • úgy, hogy \(h_{s_{i_0}}(f_{A_i}(A_{s_{i_1}}, A_{s_{i_2}}, ..., A_{s_{i_k}})) = f_{B_i}(h_{s_{i_1}}(A_{s_{i_1}}), ..., (h_{s_{i_k}}(A_{s_{i_k}}))\)
   • előző laikusan: A-n való homomorfizmus végrehajtása (formula bal oldala) után B az A leképezéseit fogja tartalmazni (formula jobb oldala)

Szignatúra algebra homomorfizmusok speciális esetei

1. Átnevezés
   • szignatúra szortjainak és műveleteinek átnevezése
2. Bővítés
   • szignatúra bővítése új szortokkal és műveletekkel
   • új szignatúra definíció a korábbi átvételével
3. Új ábrázolás
   • szignatúra átvétele, meglévő szortok helyére más szortokból képzett ábrázolások

Szignatúra algebra izomorfizmus

• 1-1 leképezés A és B között
• Jelölés: \(A \simeq B\) (A izomorf B-vel)
  • (szürjektív: minden B-beli elemhez kapcsolódik valaki)
  • (injektív: minden A-beli elem különböző B-beli elemhez kapcsolódik)
  • (bijektív: egyszerre szürjektív és injektív)
• Ha egy homomorfizmus bijektív \(\Longrightarrow\) akkor izomorfizmusról beszélünk
• Az izomorf algebrák azonosak egymással (átnevezést leszámítva)

Adattípus szignatúra algebrai megközelítésben

• Izomorfikus \(\sum\) szignatúra algebrák ekvivalencia osztálya:

\[osztály[A] = \{B \in Alg(\sum): B \simeq A\}\]

ahol

• [A]: ekvivalencia osztály
• \(B \in Alg(\sum)\): B az \(Alg(\sum)\) szignatúra algebra része
• \(B \simeq A\): B izomorf A-val

Monomorfikus és polimorfikus absztrakt típus

• Monomorfikus
  • Egyetlen adattípus tudja megvalósítani
  • Minden eleme izomorf
  • Csak egy ekvivalencia osztály van benne
• Polimorfikus
  • Több adattípus tudja megvalósítani
  • Absztrakt adattípus nem monomorfikus
  • Több ekvivalencia osztály is van benne

Specifikáció homomorfizmus

Szignatúra algebra homomorfizmus kiterjesztése a \(SPEC = (\sum, E)\) specifikációban lévő műveleti szemantikát leíró \(E\) specifikációban lévő

• változókra
• és kifejezésekre

Specifikáció változói és kifejezései leképezhetők \(\rightarrow\) másik specifikáció változóira és kifejezéseire

3. Adattípus osztály specifikációja

Adattípus osztály morfizmus diagramja

Specifikációk

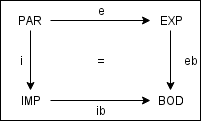
• PAR: formális paraméterek tulajdonságainak specifikációja
  • paraméteres specifikáció esetén a specifikáció részei csak akkor lesznek meghatározva \(\Longrightarrow\) amikor formális paraméterekkel példányosítjuk a specifikációt (gondolj konstruktorra)
• EXP: export felület specifikációja
  • \(EXP = PAR + (S_1, OP_1, E_1)\)
  • rajta értelmezett műveletek szintaxisának és szemantikájának definíciója
  • kitüntetett szortú specifikáció (kitüntetett szort: szort ami az adattípus elemeit azonosítja): \(EXP = (S_{EXP}, OP_{EXP}, E_{EXP})\)
• IMP: import felület specifikációja
  • \(IMP = PAR' + (S_2, OP_2, E_2)\)
  • más osztályból átvett szolgáltatások tulajdonságainak leírása
• BOD: törzsrész specifikációja
  • \(BOD = IMP + eb(EXP)\)
  • típusosztály megvalósitása, adatok reprezentálásának definíciója
  • modul rejtett része, szortok, műveletek axiómái
  • kitüntetett szortú specifikáció: \(BOD = (S_{BOD}, OP_{BOD}, E_{BOD})\)

Morfizmusok

• e: specifikációmorfizmus PAR-ből EXP-re
  • tartalmazást jelent
• i: specifikációmorfizmus PAR-ból IMP-re
  • tartalmazást és átnevezést jelent
• ib: specifikációmorfizmus IMP-ből BOD-ra
  • tartalmazást jelent
• eb: kitüntetett szortú specifikációmorfizmus EXP-ből BOD-ra
  • reprezentációt, objektumok ábrázolásával együtt megvalósuló tartalmazást jelent

Az adattípus osztályspecifikációjának részei és “szabályai”: adattípus osztály interfésze, konstrukciós része, megnyílvánulási aspektus része, megvalósítás része

1. Interfész

• osztálynév (name)
• paraméter felület (PAR)
• export felület (EXP)
• import felület (IMP)

2. Konstrukciós rész

• import felület (IMP)
• törzsrész (BOD)

3. Megnyilvánulási aspektus rész

• export felület (EXP)
• import felület (IMP)

4. Megvalósítás

• törzsrész (BOD)

4. Paraméterátadás, annak jelentése és morfizmus diagramja

Paraméteres specifikáció

• Specifikáció egyes részei akkor lesznek meghatározva \(\Longrightarrow\) ha formális paraméterekkel példányosítjuk a specifikációt

Paraméterátadás morfizmus diagramja

• PAR: paraméter specifikáció, paraméterek tulajdonságai
• e: specifikáció morfizmus
  • paraméterek specifikációjából \(\rightarrow\) export specifikációba
• EXP: export specifikáció
  • kitüntetett szortú specifikáció

Programozási nyelvekben: template-ek (C++) és generikus típusok (Java, C#)

5. Reprezentációs függvény

Adva egy adattípus absztrakt és konkrét specifikációja:

\[d_a = (A, F, E_a); \qquad d_c = (C, G, E_c);\] \[A = \{A_0, ..., A_n\}; \qquad C = \{C_0, ..., C_m\};\] \[F = \{f_0 \rightarrow A_0, ..., f_i: A_j ... A_k \rightarrow A_l, ...\}; \qquad G = \{g_0: \rightarrow C_0, ..., g_i: C_j ... C_k \rightarrow C_l, ...\};\]

ahol

• \(d_a\): adattípus absztrakt specifikációja
• \(d_c\): adattípus konkrét specifikációja
• A: absztrakt szortnevek
• C: konkrét szortnevek
• F: absztrakt műveletek
• G: konkrét műveletek

Absztrakt és konkrét objektumok egymáshoz való viszonya:

\[\varphi: C \rightarrow A\] \[\varphi = (\varphi_0, ..., \varphi_n)\] ahol \[\varphi_0: C_0 \rightarrow A_0; \varphi_1: C_1 \rightarrow A_1; ...; \varphi_n: C_n \rightarrow A_n;\]

A C objektumhalmazt az A objektumhalmaz egy reprezentánsának nevezzük az adott \(\varphi\) mellett

• ha minden \(a \in A\) objektumnak létezik legalább egy \(c \in C\) reprezentánsa
• azaz \(a = \varphi(c)\).

Ennek jelentősége kettős specifikációnál: eb megmondja hogyan reprezentáljuk IMP-el \(PAR + EXP\)-et

6. Típusöröklés

• Az öröklődéssel létrehozott osztály objektuma
• Helyettesítheti az eredeti osztály, a szuperosztály (superclass) megfelelő objektumát
• Öröklődés során azonban a szuperosztály leképezései (publikus metódusai) újradefiniálhatók
  • de csak úgy, hogy azok szintaktikai formája ne változzon meg.

Típusöröklődés definíciója:

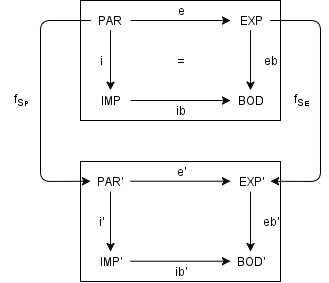
• Adva \(C = (PAR, EXP, IMP, BOD, e, i, eb, ib)\) osztályspecifikáció
• Adva \(C' = (PAR', EXP', IMP', BOD', e', i', eb', ib')\) osztályspecifikáció

Adva \(f_s = (f_{S_P}, f_{S_E})\) morfizmus:

Öröklődés morfizmus diagramja

úgy, hogy

• \(e' \circ f_{S_P} = f_{S_E} \circ e\)
• \(pt(EXP') = f_{S_E}(pt(EXP))\)

Morfizmus során az operációk szintaktikai formája megőrződik

7. Liskov féle szubsztitúciós elv

Más néven: szemantikai öröklődési követelmény

Szemantikai örkölődés \(T_1\)-ből \(T_2\)-be

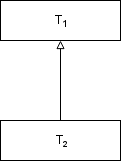
Ha a \(T_1\) típusnak minden \(o_1\) objektumához létezik a \(T_2\) típusnak egy olyan \(o_2\) objektuma, amelyre igaz a következő:

• minden olyan P programban amely \(T_1\) típusú termként van definiálva,
• a P program viselkedése nem változik meg, valahányszor az \(o_1\) objektumot \(o_2\) objektumra cseréljük ki,

\(\Longrightarrow\) akkor a \(T_2\) a \(T_1\) típus altípusa!

8. További források

• Előadás diasor