S2-01 Funkcionális nyelvek alapfogalmai

Tartalom

  1. Funkcionális nyelvek alapfogalmai
  2. Típusok
  3. Monadikus programozás
  4. További források

1.Funkcionális nyelvek alapfogalmai

1.1 Modell

Funkcionális programozási paradigma, nyelvek

Funkcionális programozás előnyei

  1. Közelebb áll a feladat és annak leírása
  2. Szemlélete közelebb áll a formális, matematikai leíráshoz, precízebb
  3. Helyességet könnyű kifejezni
  4. Feladatosztályok absztrakcióinak kifejezése
  5. Kevesebb sor, tömörebb program, kevesebb hiba, könnyebb karbantarthatóság
  6. Könnyű funkcionális programokat párhuzamosítani

Végrehajtási modell

1.2 Kiértékelés

Lusta (Lazy) kiértékelés

squareinc 7       =
square (inc 7)    =
(inc 7) * (inc 7) =
8 * (inc 7)       =
8 * 8             =
64

Mohó (strict) kiértékelés

squareinc 7     =
square (inc 7)  =
square (1 + 7)  =
square 8        =
8 * 8           =
64

1.3 Curry-zés 

((+) x) y   -- x + y helyett

1.4 Magasabbrendű függvények

Függvények, melyeknek

applyFunctionTwice :: (Int -> Int) Int -> Int
applyFunctionTwice f x = f(f x)

applyFunctionTwice (\x -> x + x) 3 = 12

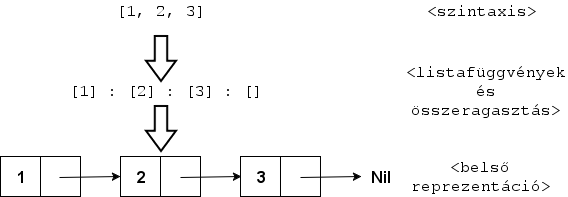
1.5 Listák

Listák ábrázolása

Lista felépítése és ábrázolása funkcionális nyelvekben.

Lista felépítése és ábrázolása funkcionális nyelvekben.

Listakonstruktor mintaillesztést használ:

                     -- "a" bármilyen típusú (polimorf) paraméter.
data [] a = []       -- Üres lista ha nem adunk elemet.
          | a : [a]  -- Értékhez hozzáragasztunk egy következő listát.
                     -- A következő lista lehet üres is ([]).

Lista típus definíciója Haskell-ban:

data List a = Nil               -- Üres lista.
            | Cons a (List a)   -- "Cons" a ragasztás, "(List a)" lehet üres is

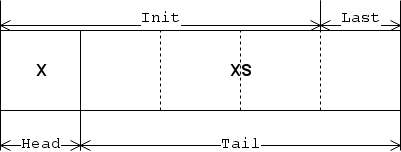
Szabványos listafüggvények (Clean nyelv)

Head, Tail, Last és Init függvények

Head, Tail, Last és Init függvények

hd [x : xs] = x                     -- Minteillesztés első elemre
hd []       = abort "hd of []"      -- Üres lista esetén hiba
tl [x : xs] = xs                    -- Minteillesztés első elem után ragasztott listára
tl []       = abort "tl of []"      -- Üres lista esetén hiba
last [x]      = x                   -- Minteillesztés egy elemre
last [x : xs] = last xs             -- Rekurzív hívás maradék listára amíg egy elemet
                                    -- nem kapunk
last []       = abort "last of []"  -- Üres lista esetén hiba
init []       = []                  -- "I didn't do anything and I still got paid."
init [x]      = []                  -- Utolsó elem a listában már nem kell
init [x : xs] = [x : init xs]       -- Rekurzív hívás amíg egy elem nincs a listában
length []       = 0                 -- Minteillesztés üres listára
length [_ : xs] = 1 + length xs     -- "_" a thunk-ot ("tönk") jelenti. Tökmindegy
                                    -- mi van ott, nem kerül kiértékelésre, nem
                                    -- foglalkozunk vele.

Magarabbrendű listafüggvények

evenNumberFunction :: Int -> Bool
evenNumberFunction x = x mod 2 == 0

evenNumbers = filter (evenNumberFunction) [0..]
map :: (a -> b) [a] -> [b]
map f [] = []
map f [x : xs] = [f x : map f xs]
foldr :: (a -> b -> b) -> b -> [a] -> b     -- (a -> b -> b): Alkalmazandó listafüggvény
foldr f z [] = z                            -- b:             Kezdőérték ami nincs listában
foldr f z (x : xs) = f x (foldr f z xs)     -- [a]:           Lista amire fold alkalmazva van
                                            -- b:             Eredményérték

További magasabbrendű listafüggvények:

1.6 Tisztaság

Pár tulajdonság:

Egyéb tulajdonságok:

2.Típusok

2.1 Algebrai adattípusok

Algebrai adattípusok: összetett típusok amiket több típusból kapjuk

Példák:

De mitől algebrai egy algebrai adattípus?

Paraméteres algebrai adattípusok

data Tree a = Node a (Tree a) (Tree a)
            | Leaf

Típus használata

fa = Node 2 (Node 1 Leaf Leaf) (Node 3 Leaf Leaf)

Lehet akár két különböző típusparamétere, a és b, ekkor kétparaméteres lesz

data Tree a b = Node b (Tree a b) (Tree a b)
              | Leaf a                        -- most Leaf-ben is tárolok értéket

Paraméternélküli adattípus

data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun

Rekurzív adattípusok

data List a = Cons a (List a)
            | Nul

Más adattípusok felírása

Például parser-ek írásához kifejezésfákat (parse tree) BNF-formában megadhatjuk

:: Statement  = Skip
              | Sequence Statement Statement
              | Assign Var ArithmeticExpression
              | If BoolExpression Statement Statement
              | While BoolExpression Statement

2.2 Típusosztályok

2.3 Típuskonstruktorok

Nulláris típuskonstruktor

Unáris típuskonstruktor

2.4 Kindok

Kind-ok nyelvtana: \[K :== * | (K \rightarrow K)\]

Kind-ok jobb asszociatívak (jobbról kezdjük a zárójelezést) \[* \rightarrow * \rightarrow * = * \rightarrow (* \rightarrow *)\]

Melyik típus milyen kind-al rendelkezik?

3.Monadikus programozás

Monad mint típusosztály

class Monad m where
    return :: a -> m a
    (>>=) infixl 1 :: (m a) (a -> m b) -> m b

    (>>) infixl 1 :: (m a) (m b) -> m b
    (>>) m k :== m >>= \_ -> k

    fail :: String -> m a

Amikor ezt a típuszosztályt akarjuk példányosítani

return

Bind művelet (>>=)

f >>= \x -> return x

>>

m >> k

(>>) m k = m >>= \_ -> k

Maybe

:: Maybe a = Just a
           | Nothing

instance Monad Maybe where
    return x = Just x
    (>>=) (Just m) k = k m
    (>>=) _ _ = Nothing

State

:: State s a = ST (S s a)     -- Clean nyelv

unST :: (State s a) -> S s a
unST (ST m) = m
instance Monad (State s) where  -- (State s) absztrakt monád, kell még s típusa
    return x = ST (return_S x)
    (>>=) m k = ST ((unST m) bind_S (\x -> unST (k x)))

List monád

instance Monad [] where
    return x = [x]
    (>>=) m k = flatten [k x \\ x <- m]

"do" jelölés

do { e1; e2 }         -- e1 >> do { e2 }

do { p <- e1; e2 }    -- e1 >>= \x -> case x of p -> do { e2 }
                      --                        _ -> fail "error"

do { let p = e1; e2 } -- let p = e1 in do { e2 }

do { e }              -- e

4.További források