A szerződésalapú programtervezés (Design by Contract, DbC) Bertrand Meyer nevéhez fűződik és a 80-as évek közepén alakult ki. A módszer három megközelítésen alapszik: a formális verifikáció, formális specifikáció, és a Hoare-hármasok.

Az elképzelés lényege, hogy a rendszer komponensek közötti együttműködésének elősegítéséhez a résztvevők kölcsönösen kötelezettségeket vállalnak, melyek segítségével biztosítva lesznek a haszonról. Ez a megközelítés nem meglepő módon az üzleti élettel hozható párhuzamba, ahol a felek az előbb említetteknek megfelelően szerződéseket kötnek.

A fenti példának megfelelően egy Objektum-orientált programban egy osztály egy szolgáltatásának három kérdésre kell választ adnia:

A szerződésalapú megvalósítás módszere

Sok programozási nyelv ad támogatást a DbC-hez hasonló technikához az assert-ek segítségével. A szerződésalapú programtervezés szerint azonban a szoftver megfelelőségéhez alapvető, hogy ezek a szerződések a tervezés szerves részét képezzék. (A gyakorlatban ez azt jelenti, hogy az assert-ek kerülnek először megírásra.) A szerződéseket egyébként meg lehet fogalmazni comment segítségével, alá lehet támasztani tesztekkel (vagy mindkettő), ha a programnyelv nem ad más támogatást.

Nyelvek melyek natívan támogatják a szerződésalapú programtervezést: Eiffel, Ada 2012, Clojure, stb.

Nyelvek melyekhez létezik third-party könyvtár: Java, C#, C, C++, Ada, JavaScript, PHP, Python, Ruby, Groovy, stb.

Ahogy az előbb már láthattuk a szerződések a legtöbb programozási nyelvben assert-ek segítségével fogalmazható meg. Azonban ha a program komponensei nem sértik meg a szerződéseket (bug-mentesek), ezek az assert-ek nem fognak hibát jelezni. Mivel ezek az ellenőrzések nagy hatással lehetnek a teljesítményre, így csak debug módban szokták őket bekapcsolni, release módban ezek a fordítás során törlésre kerülnek.

A szerződésalapú programtervezés szerint a szerződések megszegése kritikus hiba kell legyen. Ez annyit tesz, hogy a programnak hibát kell jeleznie, ha olyan dolgok történik, ami a szerződések szerint nem megengedett. Így tehát a hívó fél felelőssége lesz, hogy megfelelően működjön a program. Ezzel a szemlélettel tehát az assert-ek használata egy megfelelő megoldás lehet. Némileg ellentétes felfogás a defenzív programozás, ahol a szolgáltatónak kell felkészülnie a különböző nem megengedett esetekre és aszerint eldönteni, hogy mi történjen.

A szerződésalapú program célja, szerepe

A szerződésalapú programtervezés elsődleges célja, hogy bug-mentes OO programokat tudjunk készíteni, de több előnnyel is jár a használata:

2.Szerződések leírását támogató nyelvi eszközök az Eiffel nyelvben

Előfeltétel, utófeltétel

A szerződésalapú programtervezésben talán a legfontosabb szerepet a metódusok elő- és utófeltételei kapják. Az Eiffel nyelvben ezeket külön szintaktikus elemekkel (blokkokkal) lehet kifejezni. (Eiffelben mind az attribútumokat, mind a metódusokat feature-öknek nevezzük) Egy feature (metódus) a követekzőképp néz ki:

feature_name(...): C is -- zárójelben a paraméterek,
                        -- majd a visszatérési érték típusa
    require
        -- előfeltétel
    local
        -- lokális változók
    do
        -- implementáció
    ensure
        -- utófeltétel
    end

Az elő- és utófeltételek minden sorában egy logikai kifejezést kell írni, melyeket akár fel is cimkézhetünk:

     put (x: ELEMENT; key: STRING) is
                     -- Insert x so that it will be retrievable through key.
             require
                     container_is_not_full: count <= capacity
                     key_is_not_empty: not key.empty
             ...

A fenti példában láthatjuk, hogy egy gyűjtemény put feature-éhez megfogalmaztunk egy container_is_not_full előfeltételt, mely azt mondja ki, hogy a gyűjtemény nem lehet tele a berakás esetén, illetve egy key_is_not_empty előfeltételt, miszerint a kulcs nem lehet az üres sztring.

Az utófeltétel vizsgálata esetén már olyan vizsgálatokat is végezhetünk, melyekben a múltbéli állapotra hivatkozunk. Erre az old kulcscszót használjuk:

     put (x: ELEMENT; key: STRING) is
                     -- Insert x so that it will be retrievable through key.
             require
                -- precondition
             do
                -- implementation
             ensure
                has (x)
                item (key) = x
                count = old count + 1

Láthatjuk, hogy az utófeltételben megfogalmaztuk, hogy a feature meghívása után az elemnek a gyűjteményben kell lennie, méghozzá a kulccsal elérhetőnek kell lennie. Ezen felül az old kulcsszó segítségével ki tudtuk fejezni, hogy az új elemszámnak a régi elemszámnál eggyel nagyobbnak kell lennie.

Megjegyzés: Létezik egy strip kulcscszó is, mellyel bonyolultabb utófeltételek esetén azt tudjuk meghatározni, hogy kizárólag a felsorolt attribútumok változhatnak meg.

Osztályinvariáns

Ahogy a bevezetőben is olvashattuk, az elő- és utófeltételek mellett az osztályinvarians is fontos szerepet kap a szerződések szempontjából. Ezzel határozzuk meg egy osztály helyes állatpotainak halmazát, melyet ugyanúgy logikai állításokkal tudunk leírni. Az osztály szintaxisa Eiffelben a követekző:

class MYCLASS
create
    make -- Konstruktor feature-ök
feature {A}
    -- A osztály számára látható feature-ök
feature {B}
    -- B osztály számára látható feature-ök
invariant
    -- osztályinvariánsok
end

Az osztályinvariánst pedig egy Stack esetén például a következőképp tudjuk leírni:

class STACK[T]
creation
    make
feature
    size: INTEGER

    capacity: INTEGER
    do
        Result := data.count
    ensure
        Result > 0
    end -- capacity

feature {}

    data: ARRAY[T]

invariant
    data.lower = 1
    data.upper = capacity
    0 <= size
    size <= capacity
end -- class STACK

Ciklusok

Eiffelben a ciklusok is kiemelt figyelmet kapnak, mivel ezeknek is lehet megkötéseket, kiegészítő információkat adni. A nyelv Programozáselméletből ismert ciklus invariáns és variáns függvény kifejezésére ad lehetőséget. Egy ciklus szintaxisa a következő:

from
    -- inicializációs blokkok
invariant
    -- ciklus invariáns
until
    -- termiánálási feltétel
loop
    -- ciklusmag
variant
    -- ciklus variáns
end

A ciklus invariáns egy olyan állítás, melynek a ciklus előtt, majd minden iteráció után igaznak kell lennie.

A ciklus variáns vagy variáns függvény pedig olyan nemnegatív egész szám, melynek értéke minden iteráció után legalább eggyel csökken. Mivel egy nemnegatív egész szám nem csökkenthető a végtelenségig, illetve mivel kötelező a csökkenés így biztosítva van a terminálás. (Másként: A variáns függvény szigorúan monoton csökkenő, így el fogja érni a nullát.)

Check

A check konstrukcióval lehetőségünk nyílik az implicit feltételezések dokumentálására. Szintaxisa a követekző:

check Assertion then
    -- ...
end

Olyan esetekben például, mikor egy feature-nek egy előfeltételére nem végzünk explicit ellenőrzést, mert tudjuk, hogy teljesülni fog, akkor ezt jelezhetjük ezzel a blokkal. A check hasonló az if-hez azzal a különbséggel, hogy release módban fordítva törlésre kerül ez az ellenőrzés, illetve mindig igaz kell legyen (nem egy logikai vizsgálat, hanem egy feltétlezés). Debug módban ezen ellenőrzések jelezhetnek nekünk, ha a feltételezés mégsem teljesülne.

Bonyolultabb logikai állítások

Sok esetben fordul elő, hogy matematikailag, logikailag megfogalmazott fontos állításunk lenne egy viselkedésről, ami azonban nem kiszámolható. Ilyen például az univerzális kvantálás. Erre jó példa a legnagyobb közös osztó számítása:

lnko( a, b: INTEGER ): INTEGER is
    require    0 < a; 0 < b
    local
        tmp: INTEGER
    do
        from
            Result := a
            tmp := b
        invariant
            0 < Result; 0 < tmp;
        variant Result + tmp
        until     Result = tmp
        loop
            if Result > tmp
            then Result := Result - tmp
            else tmp := tmp - Result
            end
        end
    ensure    Result > 0; a \\ Result = 0; b \\ Result = 0;
        -- for all n: (a \\ n = 0 and b \\ n = 0) implies n <= Result
    end -- lnko

Az lnko-nak egy fontos tulajdonsága, hogy az a legnagyobb a két szám közös osztói közül, azaz:

Ezt azonban kiszámolni nem lehet, az ilyenfajta állításokat kommentekben szokták megfogalmazni.

3.A szerződések formális jelentése Hoare-hármasokkal

Ahol P és Q logikai állítások (P - előfeltétel, Q - utófeltétel), míg S utasítások sorozata. A leírás jelentése pedig:

Amennyiben P igaz S lefutása előtt és S terminál, akkor Q igaz lesz S lefutása után.

Láthatjuk, hogy a terminálás nem garantált, ezt másfajta bizonyítással érhetjük el.

Szerződések

Az eddig látott feature elő- és utófeltételek természetes módon leírhatók tehát Hoare-hármasok segítségével. Tekintsük a követekző négyzetgyök függvényt:

     sqrt (x: REAL) : REAL is
             require
                 x >= 0
             do
                -- implementation
             ensure
                Result >= 0

Ciklusok

Ciklusok esetén sok állítást fogalmazhatunk meg, mint például a ciklus invariáns vagy a variáns függvény. A követekző Hoare-hármasok igazak egy ciklusra:

4.A szerződések és a típusrendszer viszonya

Az Eiffel tisztán Objektum-orientált nyelv, így a típusrendszere is az ilyen nyelvekben megszokott, erősen típusos, típusöröklődést és polimorfizmust támogató.

Kapcsolt típus (anchored type)

Az öröklődés és polimorfizmus miatt Objektum-orientált nyelveknél sok esetben fordulhat elő az az eset, hogy nem ismerjük az egyes változók dinamikus típusát fordítási időben. Ez az ismeret viszont sok esetben fontos lenne. Gondoljunk csak például arra az esetre, mikor síelő fiúkat és lányokat akarunk elszállásolni, viszont csak az azonos neműeket szeretnénk egy szobába tenni. Ezt a típusokkal tudjuk elérni a követekző módon:

class SKIER
feature
    roommate: like Current

    share( other: like roommate ) is
    require
        other /= Void
    do
        roommate := other
    ensure
        other = roommate
    end
end

Láthatjuk, hogy a roomate attribútum típusa like Current azaz meg kell egyezzen az aktuális típussal (A Current az aktuális objektumot jelöli. Olyan, mint Java-ban a this.). Ez azt jelenti, hogy ha egy GIRL osztályt leszármaztatunk a SKIER osztályból, akkor annak a roomate attribútumoka is GIRL típusú kell legyen. Emellett láthatjuk, hogy a share metódus paramétere like roomate típusú, magyarul csak olyan objektumot adhatunk paraméterként, mely megegyezik a roomate típusával. (GIRL esetén csak GIRL lehet)

Megjegyzés: Létezik kiskapu, van lehetőségünk fiúkat és lányokat egy szobába rakni. Ezt a kiskaput "Polymorphic CAT-call"-nak hívják.

Expandált és referencia típusok

Eiffelben lehetőségünk van meghatározni, hogy egy típus érték vagy referencia típus legyen. Alapvetően referencia típusúak az osztályaink, de az expanded kulcsszóval érték típusúvá alakíthatjuk őket:

expanded class PONT
feature

    x,y: REAL

    eltol( dx, dy: REAL )
    do
        x := x + dx
        y := y + dy
    end -- eltol

end --class PONT

Ebben az esetben természetesen más nyelvekhez hasonlóan figyelembe kell venni a paraméterátadásokat, értékadásokat, stb., ugyanis ezekben az esetekben a példány másolódik.

Deferred

Más nyelvekből ismert abstract tulajdonságot megfogalmazhatunk Eiffelben. Erre a deferred kulcsszó használható. Ahogy megszoktuk, amennyiben legalább egy feature deferred egy osztályban, az adott osztály is automatikusan deferred kell legyen. Ezenkívül Eiffelben lehetőségünk van arra, hogy a szerződést megfogalmazzuk és csak az implementációt tegyük deferred-dé:

deferred class VEHICLE feature
    dues_paid (year: INTEGER): BOOLEAN is
         do ... end
    valid_plate (year: INTEGER): BOOLEAN is
         do ... end
    register (year: INTEGER) is
            -- Register vehicle for year.
         require
             dues_paid (year)
         deferred
         ensure
             valid_plate (year)
         end
end -- class VEHICLE

Attól függetlenül, hogy egy motornak és egy autónak más a regisztrációs eljárása, az elő- és utófeltételeik megegyeznek. Ezeket meghatározhatjuk a jármű szintjén, így a leszármazottakban csak az implementációt kell megírnunk.

5.Szerződések és objektum-orientáltság: öröklődés és felüldefiniálás

Öröklődési gráf

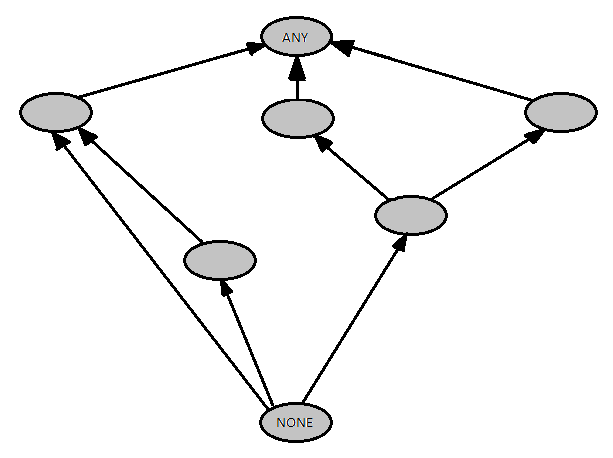
Az Eiffel támogatja a többszörös öröklődést, így lehetőség van egy különleges öröklődési gráf kialakítására.

Minden osztály az ANY osztályból származik. A NONE egy fiktív osztály mely minden osztályból öröklődik, mindennek altípusa.

Láthatóságok

Egy osztály feature-einek láthatóságát (export status) osztály szinten tudjuk korlátozni. Ez azt jelenti, hogy meg tudjuk határozni, hogy egy feature egy konkrét osztály (és annak leszármazottai) számára látható:

class MYCLASS
    ...
    feature {A}
        -- A osztály számára látható feature-ök
    feature {B}
        -- B osztály számára látható feature-ök
    feature {ANY}
        -- Minden osztály számára látható (public)
    feature {NONE}
        -- Senki számára nem látható (private)
    ...
end

Többszörös öröklődés, átnevezés

A több osztályból való öröklés egyik legnagyobb kérdése az ún. diamond inheritance, melyre különböző nyelvek más-más megoldást adnak. Eiffelben sok lehetőség van az ősosztály megörökölt metódusainak kezelésére, hogy el tudjuk kerülni a névütközést.

class
    LINKED_QUEUE [G]
inherit
    QUEUE [G]
        undefine
            is_empty,
            copy,
            is_equal
        redefine
            linear_representation,
            prune_all,
            extend
        select
            item,
            put
        end
    LINKED_LIST [G]
        rename
            item as ll_item,
            remove as ll_remove,
            make as ll_make,
            remove_left as remove,
            put as ll_put
        export
            {NONE}
                all
            {ANY}
                writable,
                extendible,
                wipe_out,
                readable
        undefine
            fill,
            append,
            prune,
            readable,
            writable,
            prune_all,
            extend,
            force,
            is_inserted
        redefine
            duplicate,
            linear_representation
        select
            remove
        end

A fenti példában a LINKED_QUEUE-t láthatjuk, ami a LINKED_LIST és a QUEUE osztályokból származik. Az ősosztályok metódusait pedig különféle módon kezeli, melyek a követekzők:

Kovariancia, kontravariancia

Az öröklődés és polimorfizmus talán legnagyobb kérdése a variancia. A variancia két típus helyettesíthetőségét fejezi ki.

Kovarianciának nevezzük, ha az általánosabb típus (A) helyére a speciálisabb típust (B) behelyettesíthetjük.

Kontravarianciának nevezzük, ha a speciálisabb típus (B) helyére az általánosabb típust (A) helyettesíthetjük be.

Invariáns vagy Nonvariáns a reláció, ha a fentiek közül egyik sem mondható.

A fent említett tulajdonságok kontextustól függőek. A legfontosabb felhasználási területe ezeknek a tulajdonságoknak az öröklődés során a metódusok specializációja. Egy metódust akkor tudunk típushelyesen specializálni, ha a paraméterei kontravariánsak az ősosztály metódusának paramétereivel, míg a visszatérési típusa kovariáns a ősosztály metódusának visszatérési típusával.

Tegyük fel, hogy CREATURE :> ANIMAL :> MONKEY és FOOD :> FRUIT :> BANANA, illetve létezik egy osztályunk:

class ANIMAL_FEEDER 
create
    make
feature {ANY}
    feed(a : ANIMAL) : FRUIT
    do 
        -- implementation
    end
end

Ha létre akarjuk hozni a MY_FEEDER osztályt és specializálni szeretnénk a feed metódust, akkor a paramétere lehet továbbra is ANIMAL típusú, vagy CREATURE, de MONKEY semmiképp. Ugyanis azon a helyen, ahol kicseréljük az ANIMAL_FEEDER példányt, az azt használók nem feltétlenül csak MONKEY típusú paramétereket adhatnak át. Hasonlóképpen a visszatérési érték csak FRUIT és BANANA lehet. Az ANIMAL_FEEDER-t használók FRUIT típust vagy annak altípusait várják értékül.

Szerződések

Ahogy a metódusok paramétereire és visszatérési értékére, a szerződésekre is érvényes a variancia. A feature-ök előfeltételeit lazítani lehet, míg az utófeltételeit megszorítani. Erre a require else és ensure then kulcsszavakat lehet használni. A require else esetén az újonnan megfogalmazott előfeltétel vagy kapcsolatban fog állni az eredetivel. Az ensure then esetén az utófeltétel szigorodik, és kapcsolatban fog állni az eredeti utófeltétellel.

Osztályinvariáns

Az öröklődés során Eiffelben a leszármazottak megőrzik az ősök osztályinvariansait. Így a leszármazott invariánsa a leszármazottban megfogalmazott invariáns és ősei invariánsának konjunkciója lesz (össze és-elődnek).

6.Üres referenciák

Referencia típusok esetén a nullreferencia kérdése, illetve a nullable típusok természetesen Eiffelben is felmerülnek. A nullreferencia Eiffelben Void névre hallgat. A nullable vagy non-nullable tulajdonságok egy változó típusának meghatározásánál kapnak szerepet. A nullable Eiffelben detachable, míg a non-nullable attached kulcsszavakkal fejezhető ki.

    my_attached_string: STRING
    my_detachable_string: detachable STRING

            ...

        my_attached_string := my_detachable_string    -- Invalid
        my_detachable_string := my_attached_string    -- Valid

A fenti példában láthatjuk, hogy milyen módon feleltehetők meg egymásnak az attached és detachable változók, illetve, hogy alapvetően minden változó attached.

7.Kivételek

Eiffelben a kivételek eltérnek a más nyelvekben megszokottaktól. Semmiképpen nem részei a control-flownak, tényleg csak speciális esetekben léphetnek fel:

A metódusok definíciójánál meg lehet fogalmazni egy rescue klózt, mely kivétel fellépésénél fut le. Ebben a klózban hozhatjuk újra az invariánsnak megfelelő állapotba a példányunkat. Ezek kívül lehetőségünk van a retry kulcsszóval az adott metódust újra próbálni. A rescue blokk lefutása után a metódus vagy sikerrel lefut, vagy kivételt vált ki az őt hívó rutinban.

attempt_transmission (message: STRING) is
        -- Try to transmit message, at most 50 times.
        -- Set successful accordingly.
    local
        failures: INTEGER
    do
        if failures < 50 then
            transmit (message); successful := true
        else
            successful := false
        end
    rescue
        failures := failures + 1
        retry
    end

S2-03 A szerződésalapú programtervezés

Tartalom

1.A szerződésalapú programtervezés és -megvalósítás módszere, célja, szerepe

A szerződésalapú programtervezés módszere

A szerződésalapú megvalósítás módszere

A szerződésalapú program célja, szerepe

2.Szerződések leírását támogató nyelvi eszközök az Eiffel nyelvben

Előfeltétel, utófeltétel

Osztályinvariáns

Ciklusok

Check

Bonyolultabb logikai állítások

3.A szerződések formális jelentése Hoare-hármasokkal

Szerződések

Ciklusok

4.A szerződések és a típusrendszer viszonya

Kapcsolt típus (anchored type)

Expandált és referencia típusok

Deferred

5.Szerződések és objektum-orientáltság: öröklődés és felüldefiniálás

Öröklődési gráf

Láthatóságok

Többszörös öröklődés, átnevezés

Kovariancia, kontravariancia

Szerződések

Osztályinvariáns

6.Üres referenciák

7.Kivételek

8.További források